Margin Infused Relaxed Algorithm

Margin Infused Relaxed Algorithm (MIRA)^[1] is a machine learning algorithm, an online algorithm for multiclass classification problems. It is designed to learn a set of parameters (vector or matrix) by processing all the given training examples one-by-one and updating the parameters according to each training example, so that the current training example is classified correctly with a margin against incorrect classifications at least as large as their loss.^[2] The change of the parameters is kept as small as possible.

A two-class version called binary MIRA^[1] simplifies the algorithm by not requiring the solution of a quadratic programming problem (see below). When used in an one-vs.-all configuration, binary MIRA can be extended to a multiclass learner that approximates full MIRA, but may be faster to train.

The flow of the algorithm^[3]^[4] looks as follows:

Algorithm MIRA
  Input: Training examples 
  Output: Set of parameters

   ← 0,  ← 0
  for  ← 1 to 
    for  ← 1 to 
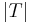
       ← update  according to 
       ← 
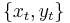
    end for
  end for
  return

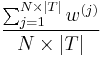
"←" is a loose shorthand for "changes to". For instance, "largest ← item" means that the value of largest changes to the value of item.
"return" terminates the algorithm and outputs the value that follows.

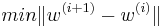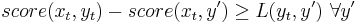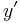The update step is then formalized as a quadratic programming^[2] problem: Find $min\|w^{(i%2B1)} - w^{(i)}\|$ , so that $score(x_t,y_t) - score(x_t,y')\geq L(y_t,y')\ \forall y'$ , i.e. the score of the current correct training $y$ must be greater than the score of any other possible $y'$ by at least the loss (number of errors) of that 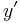$y'$ in comparison to $y$ .

References

^ ^a ^b Crammer, K., Singer, Y. (2003): Ultraconservative Online Algorithms for Multiclass Problems. In: Journal of Machine Learning Research 3, 951-991. http://jmlr.csail.mit.edu/papers/v3/crammer03a.html
^ ^a ^b McDonald, R., K. Crammer and F.C.N. Pereira (2005): Online Large-Margin Training of Dependency Parsers. In: Proceedings of the 43rd Annual Meeting of the ACL, pp. 91-98. http://aclweb.org/anthology-new/P/P05/P05-1012.pdf
^ Wanatabe, T. et al (2007): Online Large Margin Training for Statistical Machine Translation. In: Proceedings of the 2007 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, 764–773.
^ Bohnet, B. (2009): Efficient Parsing of Syntactic and Semantic Dependency Structures. Proceedings of Conference on Natural Language Learning (CoNLL), Boulder, 67-72.